Die Physik einer Achterbahn
Es gibt verschiedenen Antriebstechniken, die bei einer Achterbahn angewendet werden können. Sobald eine Achterbahn durch solch ein Antriebssystem in Bewegung gesetzt wurde, wird der restliche Verlauf der Achterbahn allein durch die Schwerkraft geregelt.
Der Start
Umso höher die erste Steigung, desto mehr potentielle Energie ist vorhanden und demnach ist auch mehr Energie für die darauffolgende Achterbahnfahrt, welche dann zum Beispiel länger sein kann.
Da auf moderne Achterbahnen das vorgestellte Antriebssystem „Start durch einen Linearmotoren“ angewendet wird, ist es nun auch interessant, wie man mithilfe der zur Verfügung stehenden Angaben die beschleunigte Bewegung sowie die Beschleunigungsstrecke errechnen kann.
Der Blue Fire Megacoaster im Europa-Park ist aktuell die modernste Achterbahn in Deutschland, auf der diese Antriebstechnik angewendet wird. Er beschleunigt von 0 auf 100 km/h in 2,5 Sekunden. Mit diesen Angaben lassen sich nun die Beschleunigung „a“ sowie die Beschleunigsungstrecke „s“ des Megacoasters berechnen.
Berechnung der Beschleunigung

Gegeben sind:
t = 2,5 Sekunden sowie v = = 27,78
Es gilt für die gleichförmige Beschleunigung:
a =
a =
a = 11,1
Der Achterbahnzug wird also pro Sekunde um 11,1 schneller. Umso interessanter ist es nun natürlich, welche Belastung auf unserem Körper wirkt. Die normale Erdbeschleunigung beträgt 9,81 . Rechnet man nun mit den 11,1 und teilt diese durch die Erdbeschleunigung erhält man die g-Kraft mit der der Mensch bei dieser Beschleunigung in den Sitz gedrückt wird.
= 1,1 g
Die Fahrgäste werden also mit dem 1,1-fachen ihres Körpergewichts in den Sitz gedrückt.
Berechnung der Beschleunigungsstrecke

Dadurch, dass wir die Beschleunigung ausgerechnet haben, können wir mithilfe des Weg-Zeit-Gesetzes nun auch die Beschleunigungsstrecke „s“ berechnen.
s = a t2
s = 11,1 6,25 s²
s = 34,7 m
Interessant ist es nun natürlich meine durch die Rechnung erfahrenen Werte mit denen aus der Realität zu vergleichen. Auf der Website der Achterbahn steht eine Beschleunigungstrecke von 80 Metern. Das ist zu meinem Ergebnis eine Differenz von 45,3 Metern. Mit dieser großen Differenz habe ich mich nicht zufrieden gegeben und habe begonnen herauszufinden, wieso solch eine große Differenz zum realen Wert gegeben ist. Ich habe mich mit einer E-Mail an den Achterbahnhersteller der Achterbahn (Mack Rides GmbH & Co KG) gewendet. Als Antwort bekam ich folgendes:
„Hallo,
hier meine Anmerkungen zu Ihrer Rechnung. Die Beschleunigungsstrecke ist tatsächlich 80 Meter lang. Je nach Beladung, Wind etc. benötigen wir ca. die Hälfte der Strecke für die tatsächliche Beschleunigung. Danach wird die Geschwindigkeit gemessen und mit der vorgegebenen Geschwindigkeit verglichen, bis die Ausgangsgeschwindigkeit erreicht ist. Im Falle eines Roll-Back nutzen wir diese Strecke auch für die Bremsung. (Roll-Back heißt, wenn bei einem Antrieb durch Linearmotoren die Kraft nicht ausreicht um den Zug über den Höchsten Punkt zu katapultieren und der Zug wieder in die Station zurück rollt). Hier möchten wir natürlich nicht dass das Fahrzeug bis in den Bahnhof zurückfährt sondern dass wir es innerhalb der Beschleunigungsstrecke abgebremst wird.
Die 80m sind von den Fakten also korrekt. Ihre Rechnung allerdings ebenso.
Einen weiteren Hinweis habe ich von einem unserer Ingenieure erhalten. Sie gehen von einer konstanten Beschleunigung aus. Wir haben hier aber eine asymptotische Beschleunigung. Wir beginnen mit 1G Beschleunigung die dann immer weniger wird. Daher kommen Sie mit ihrer Rechnung auch nicht ganz hin.
Ich hoffe das hilft Ihnen zumindest in Etwa weiter.“
Diagramme
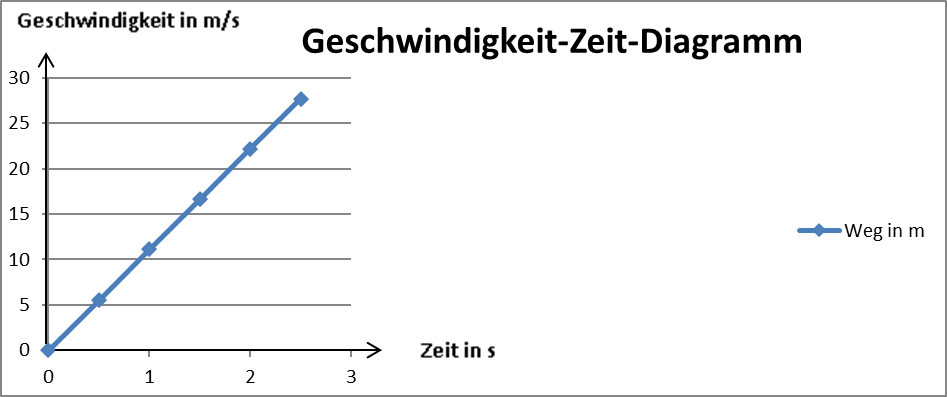
Das Geschwindigkeit-Zeit-Diagramm zeigt, dass die Geschwindigkeit pro Sekunde um 11,1 m/s zunimmt. Die Geschwindigkeit v ist also proportional zur Zeit.
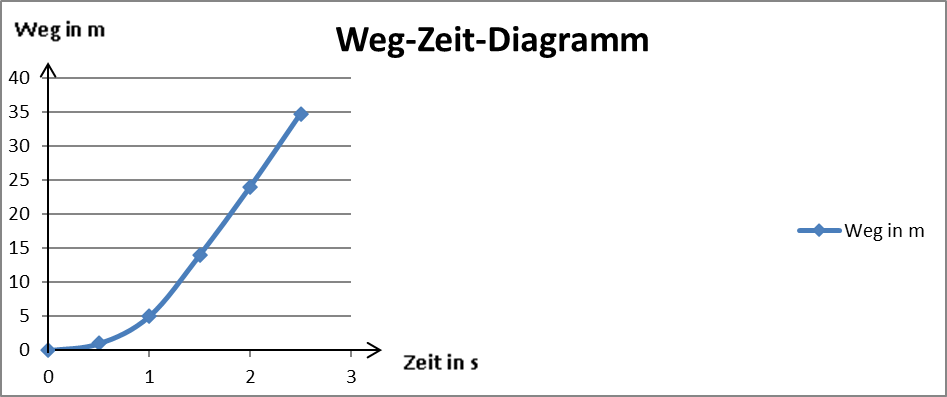
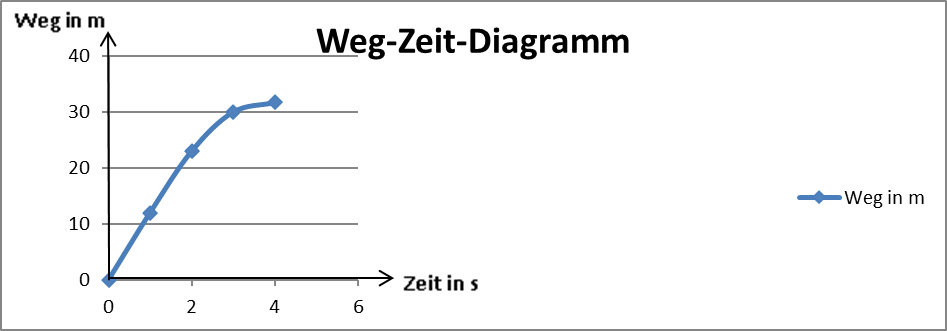
Das Weg-Zeit-Diagramm zeigt, dass der zurückgelegte Weg „s“ proportional zum Quadrat der Beschleunigungszeit ist.
Energieumwandlungen
Am Beispiel einer Achterbahnfahrt kann man sehr gut Energieumwandlungen erklären.
„Mechanische Energie kann einem System zugeführt werden, indem man einen Körper beschleunigt oder ihn hochhebt oder auch indem man eine Feder spannt. In jedem dieser Fälle wird die Energie im neuen System in einer bestimmten charakteristischen Form gespeichert“.
Betrachten wir unsere Achterbahnstrecke also als ein System, dem Energie zugeführt wird. Es gibt zwei Energiearten, die bei einer Achterbahn von wichtiger Bedeutung sind. Zum einen gibt es die kinetische Energie, auch Bewegungsengerie genannt [Ekin = (1/2) m v2] und zum anderen die potentielle Energie, auch Lageenergie genannt [Epot = m g h].
Einem Achterbahnzug wird am Anfang potentielle Energie (Lageenergie) zugeführt. Dies geschieht durch die verschiedenen Antriebsarten einer Achterbahn mithilfe von elektrischer Energie. Hat ein Achterbahnzug nun durch Katapultstart oder Kettenlift den höchsten Punkt erreicht, so wird die potentielle Energie, die wie beschrieben dem Achterbahnzug zugeführt wurde, in kinetische Energie in Form von Bewegungsenergie umgesetzt. Hat der Achterbahnzug nun wieder einen Punkt erreicht, wo er wieder nach oben fährt, so findet wieder eine Umwandlung von der potentiellen Energie in kinetische Energie statt.
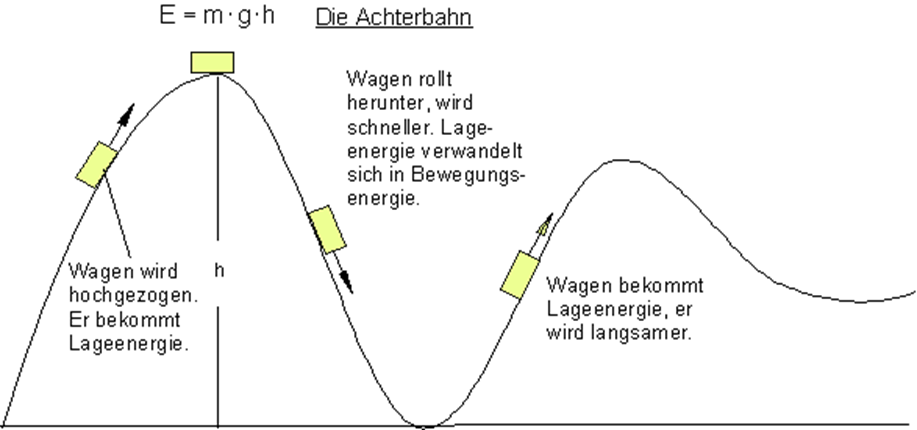
Interessant ist es nun natürlich herauszufinden, welche Geschwindigkeit der Wagen am ersten tiefen Punkt kurz vor der Energieumwandlung besitzt. Mit den Formeln der kinetischen sowie potentiellen Energie kann man diese Geschwindigkeit herausfinden.
Wir nehmen ein existierendes Beispiel. Die Achterbahn „Silver Star“ besitzt eine maximale Höhendifferenz von 65 Metern. Den höchsten Punkt erreicht der Silver Star mit einer Kettengeschwindigkeit von 16,2 km/h = 4,5 m/s. Wie schnell ist der Silver Star nun an der ersten, tiefsten Stelle? [vgl. [13]].
EHügel = ETal
Ekin, Hügel(H) + Epot, Hügel(H) = Ekin, Tal(T) + Epot, Tal(T) + WReibung
= 130 km/h
Im ersten Talpunkt erreicht der Achterbahnzug des Silver Stars also eine Geschwindigkeit von 36 m/s = 130 km/h. Auf der Informationsseite steht eine gemessene Maximalgeschwindigkeit von 127 km/h. Zu dem Ergebnis ist das eine Differenz von 3 km/h. Es kam ein leicht unterschiedliches Ergebnis raus, da die Reibung nicht beachtet wurde. Da uns leider keine Daten für die Reibung bei der Achterbahn vorliegen und auch auf Nachfrage bei dem Achterbahnhersteller keine Informationen dazu herausgefunden werden konnten, konnte ich dies nicht mit in meine Rechnung einfließen lassen [vgl. [13]].
Perpetuum mobile ist das Stichwort: Ein System, was wenn es einmal in Gang gesetzt wird, ewig in Bewegung bleibt. Wieso kann der zweite Hügel einer Achterbahn nicht genauso hoch wie der erste sein? Es gibt Einflüsse, die dies beinträchtigen. Der größte Einfluss ist die Reibungsenergie, die durch die Reibung der Fahrbahn und der Achterbahnräder entsteht.
Bremsvorgang
Welche verschiedenen Methoden es gibt, um den Bremsvorgang einzuleiten, sowie deren Funktion wurden unter dem Punkt 2.2.3 behandelt. Nun gilt es diesen Vorgang physikalisch zu erklären. Erst wurde die Beschleunigung für den Start berechnet. Nun gilt es für den Bremsvorgang die verzögerte Beschleunigung zu berechnen.
Wir nehmen als Rechenbeispiel wieder eine Achterbahn aus dem Europa-Park. Der „Silver Star“ ist zwar nicht die modernste Achterbahn, er besitzt jedoch ein Bremssystem aus Wirbelstrom, sowie Reibbremsen. Durch die Wirbelstrombremsen wird der Achterbahnzug von „Silver Star“ innerhalb von 4 Sekunden von 50km/h auf ca 7 km/h abgebremst. Mit diesen Werten können wir die verzögerte Beschleunigung „aB“ berechnen [vgl. [13]].
Gegeben sind: t = 4 s und v(t) = 50 v0= 7
v = 50 7 = 43 = 11,94
aB =
aB = 11,94
aB = 3
Das Ergebnis bedeutet, dass der Zug pro Sekunde um 3 langsamer wird. Umso interessanter ist es nun natürlich zu erklären, welche Belastung auf unserem Körper wirkt. Die normale Erdbeschleunigung beträgt ungefähr 9,81 = 1g. Rechnet man nun mit den 3 und teilt diese durch die Erdbeschleunigung erhält man die g-Kraft mit der der Mensch bei dieser Beschleunigung gegen die Sicherheitsbügel gedrückt wird.
= 0,31 g
Die Fahrgäste werden also mit dem 0,31-fachen ihres Körpergewichts nach vorne gegen den Sicherheitsbügel gedrückt.
Berechnung der Bremsstrecke
Die Bremsstrecke berechnen wir mit folgender Formel:
Gegeben sind: v0= 7
s(t) = 31,76 Meter
Aus dieser Rechnung ergibt sich also eine Bremsstrecke von 31,76 Metern.
Diagramme
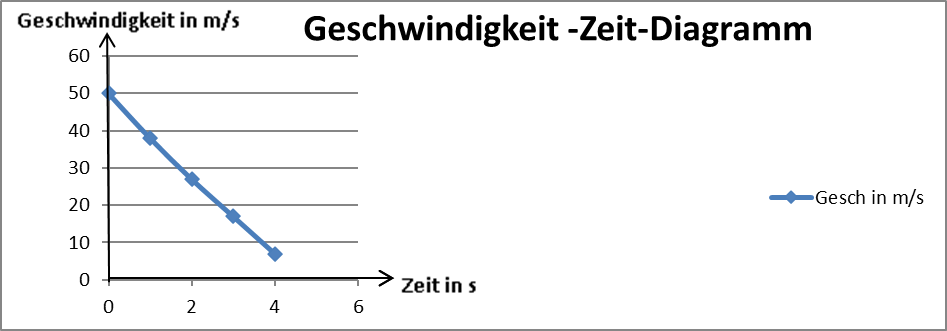
Das Weg-Zeit-Diagramm der verzögerten Beschleunigung zeigt noch mal, dass die Geschwindigkeit pro Sekunde um 3 m/s abnimmt. Die Geschwindigkeit „v“ ist also proportional zur Zeit.
Beschleunigungskraft
„Beim freien Fall erfahren alle Körper am selben Ort die gleiche konstante Fallbeschleunigung. Sie ist gleich dem Ortsfaktor g. Stets gilt G= m g“ [aus [16], Seite 33].
Ohne diese sogenannte Erdanziehungskraft wäre unser Leben nicht vorstellbar. Sie sorgt dafür, dass wir Menschen auf dem Boden laufen und nicht wie im Weltraum schweben. Weiterhin hat die Erdanziehungskraft eine wichtige Bedeutung bei der Achterbahn. Sie sorgt erstens dafür, dass eine Achterbahn überhaupt funktioniert, nämlich wenn ein Achterbahnzug an der Spitze angekommen ist, dass er durch die Erdanziehung nach unten fährt. Die normale Erdanziehungskraft beträgt ungefähr 9,81 = 1g. Bei der Achterbahn treten Beschleunigungskräfte auf und spricht man von einer Beschleunigungskraft von 1g, so entspricht das der normalen Erdanziehung.
Bei einer Achterbahnfahrt werden zwei wichtige Beschleunigungskräfte unterschieden.
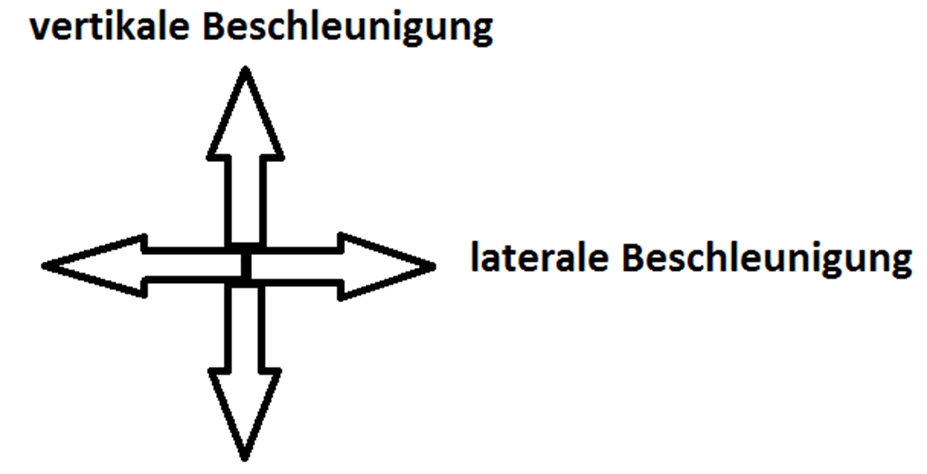
Die vertikalen Beschleunigungskräfte sorgen dafür, dass ein Fahrgast bei einer Achterbahnfahrt in den Sitz nach unten gedrückt wird oder im Gegenteil aus dem Sitz nach oben fliegt. Die lateralen Beschleunigungskräfte sorgen dafür, dass ein Fahrgast seitlich aus dem Sitz gedrückt wird. Damit die Fahrgäste trotz dieser Kräfte eine sichere Fahrt erleben können, dafür gibt es das Fahrgastbügelsystem.
Die erste Frage ist nun, wie entsteht diese Kraft, die eine Achterbahnfahrt so aufregend gestaltet? Die Lösung findet man in der Trägheit der Masse.
„Alle Körper behalten ihren Bewegungszustand bei, wenn dieser nicht von außen durch Kräfte geändert wird: Körper sind träge. Wenn ein Körper seinen Bewegungszustand (Richtung bzw. Schnelligkeit) ändert, so wird dies durch andere Körper also durch Kräfte von außen erzwungen)“ [aus [16], Seite. 11].
Vertikale Beschleunigungskraft
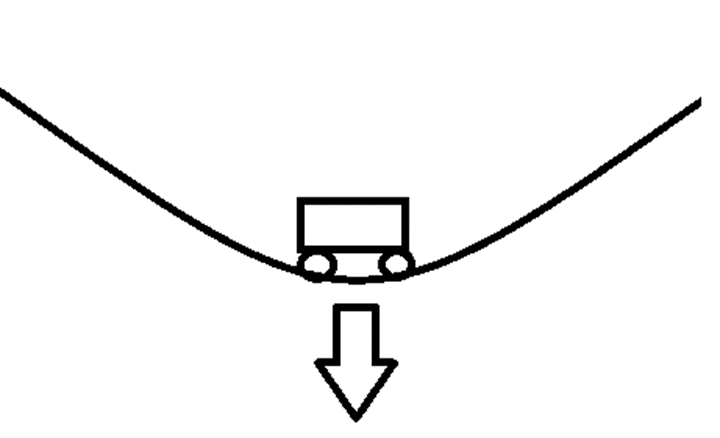
Es wird zwischen negativer und positiver vertikalen Beschleunigung unterschieden. Fährt eine Achterbahn steil nach oben und wechsel durch einen Hügel innerhalb kürzester Zeit die Fahrt von oben nach unten, so möchte der menschliche Körper seine Bewegungsrichtung beibehalten, kann dies aber nicht, da er nach unten gedrückt wird. Dieser Effekt sorgt dann bei dem Fahrgast für die negative vertikale Beschleunigung und man hat das Gefühl zu schweben, da man nur von dem Fahrgastbügelsystem im Sitz gehalten wird. Dieses Gefühl nennt sich Schwerelosigkeit.
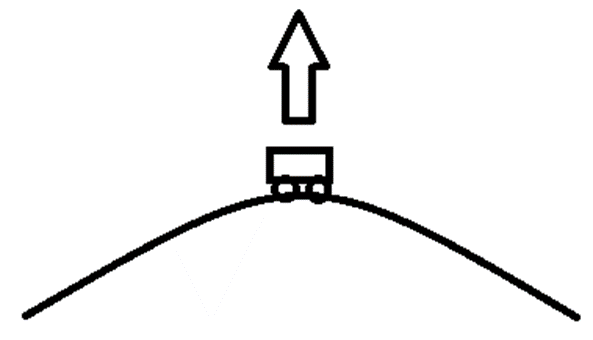
Im umgekehrten Fall kommt der Achterbahnzug von einem Hügel unten im Tal an und fährt gleich wieder nach oben. Der Fahrgast möchte aber nach dem Trägheitsgesetz weiterhin nach unten und erfährt die positive vertikale Beschleunigung. Er wird in den Achterbahnsitz nach unten gepresst und fühlt sich schwerer, da eine mehrfache g-Kraft auf ihn wirkt.
Wie groß die vertikale Beschleunigung ist, wird durch den Radius der Hügel und Täler beeinflusst.
Welchen großen Einfluss die Neigung des Tales auf die g-Kraft hat, lässt sich in einem schönen Experiment beweisen. „No Limits Coaster“ ist ein Achterbahnsimulationsprogramm, welches von Achterbahnherstellern für die Planung von Achterbahnen genutzt wird. Es ist im Handel für wenig Geld erhältlich und da ich mich schon seit mehreren Jahren mit dem Bau von Achterbahnen beschäftige, besitze ich dieses Simulationsprogramm. Mit dem Programm kann man verschiedenste Achterbahnen bauen, sowie im Nachhinein fahren und sehen, welche Belastungen auf den Fahrgast wirken.
In meinem Experiment zur vertikalen Beschleunigung habe ich zwei unterschiedliche Täler gebaut. Beim ersten Tal ist der Radius beim Durchfahren größer gewählt. Welche Auswirkung hat das nun bei gleicher durchfahrender Geschwindigkeit?
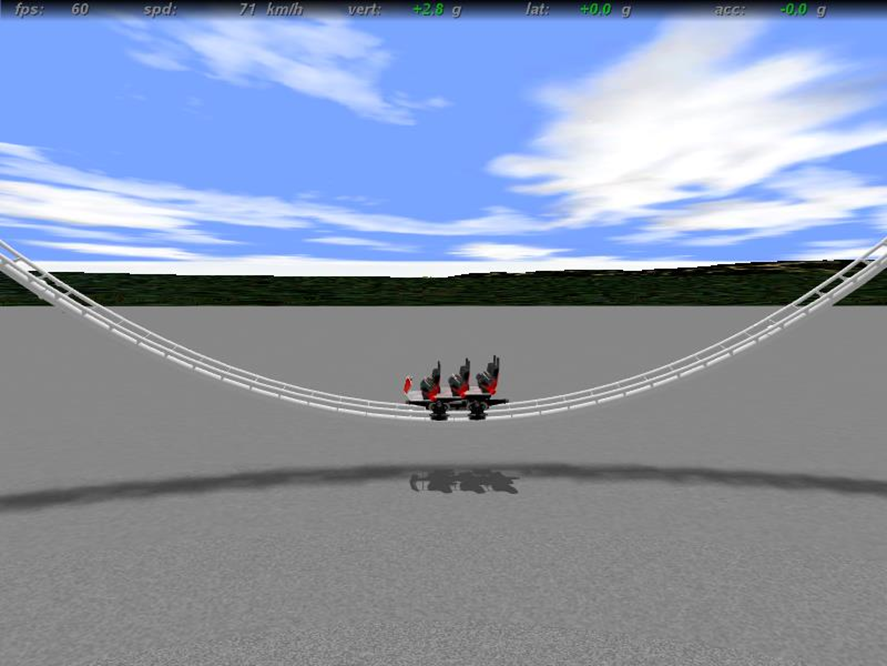
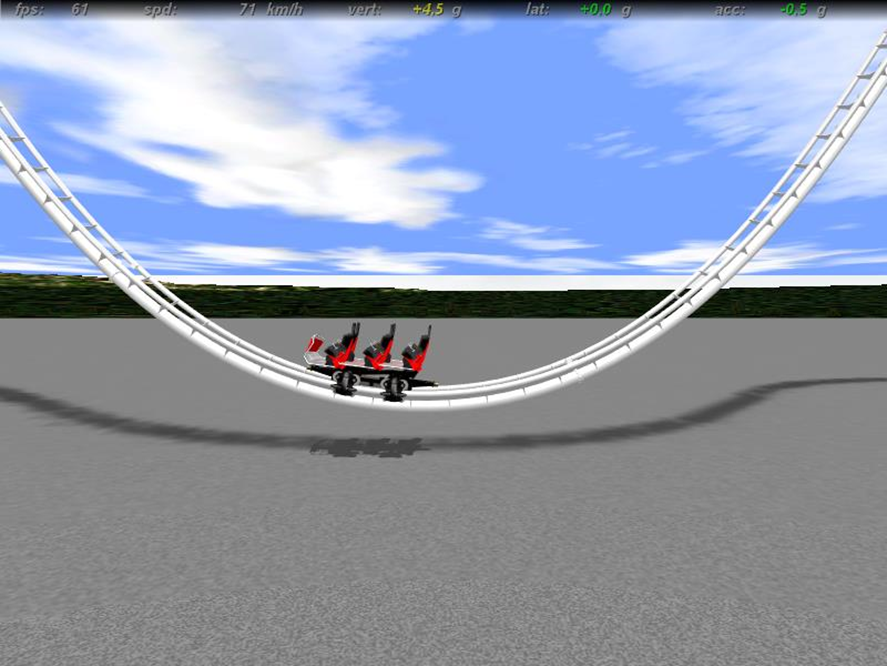
Bei dem Experiment kann man sehr schön erkennen, dass ein engerer Radius eine höhere positive vertikale Beschleunigungskraft zur Folge hat. Bei meiner Simulation erhalte ich einen Wert von +2,8g. Bei der anderen Simulation erreiche ich dagegen einen Wert von +4,5g, dieser Wert nähert sich schon der kritischen Grenze für die Belastbarkeiten, die ein Mensch ohne Verletzungen aushält. Solche Aspekte müssen beim Bau einer Achterbahn vorher berechnet und beachtet werden.
Laterale Beschleunigungskraft
Wie man gut erkennen kann, gibt es bei der Fahrt auf der Geraden keine laterale Beschleunigungskraft (Grüne Markierung).
Laterale Beschleunigungskräfte treten auch nur auf, sobald der Achterbahnwagen eine Kurve durchfährt. Dies lässt sich wieder mit dem Trägheitsgesetz beschreiben. Fährt der Fahrgast von einer geraden Strecke in eine Kurve, möchte dieser den Zustand von der geraden Strecke beibehalten und wird so durch die Kurve nach außengedrückt.

Dieser Effekt bei einer Achterbahn ist unangenehmer für den Fahrgast als die vertikale Beschleunigung. Deswegen werden die lateralen Kräfte bei den meisten Achterbahnen mithilfe von einer Neigung der Schiene unterdrückt. So ist der Übergang in eine Kurve viel sanfter, nicht so ruckartig und der Fahrgast erfährt nur minimale laterale Beschleunigung. Welchen Unterschied solch eine Neigung der Achterbahnschiene macht, lässt sich wieder schön mit der Achterbahnsimulation „No Limits“ beweisen.

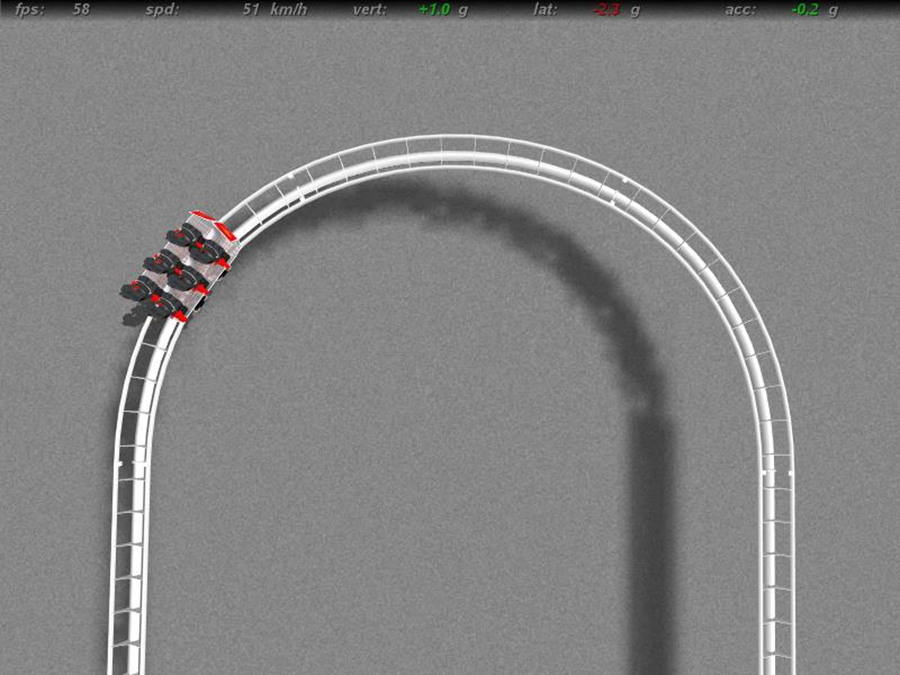
In der oberen Abbildung ist die laterale Beschleunigung durch die Neigung der Kurve minimal, während in der unteren Abbildung eine Achterbahnfahrt mit einer großen lateralen Beschleunigung darstellt.

Diese laterale Beschleunigung wird zum Beispiel bei dem Achterbahntyp „Wilde Maus“ genutzt. Die „Wilder Maus“ ist eine der wenigen Achterbahnen, bei der die lateralen Kräfte dafür genutzt werden, um den Fahrgast ein Gefühl des seitlichen Entgleisens des Achterbahnwagens zu geben. Der Radius der Kurve ist sehr eng gewählt.
Mehr zum Thema Achterbahnen, deren Technik und die Belastung auf den menschlichen Körper
- Die Welt der Freizeitparks und Achterbahnen
- Die Geschichte der Achterbahn
- Die Technik einer Achterbahn
- Sicherheitssysteme einer Achterbahn
- Die Physik einer Achterbahn
- Beschleunigungskräfte einer Achterbahnfahrt
- Die Rentabilität einer Achterbahn
- Interview mit einem Achterbahnhersteller
- Bau einer Modellachterbahn
- Achterbahnfahrt und Auswirkung auf den Menschen
- Belastbarkeit bei einer Achterbahnfahrt
- Das Gleichgewichtsorgan
- Adrenalin
- Herzfrequenz und Herzrasen
Keine Kommentare
Entschulidge, für diesen Artikel wurde die Kommentarfunktion deaktiviert.